Colour gradients

Gradients implemented below have the same interfaces:

• lut the lookup table with linear interpolation contains colour stops for the gradient.
• start_point the start point of the gradient, that can be a center of the gradient in depends on gradient type.
• end_point the end point of the gradient, that can represent a direction for an angular gradient or maximal radius of radial and diamond.

Linear

The linear gradient is a smooth transition of color along a line. To create the linear gradient you must define at least two color stops. You can also set two points between which the gradient will be drawn.

norm = end_point - start_point
max_dist = normalize(norm)
for each[i, j]:
    cur_point = [i, j] - start_point
    f = dot(norm, cur_point) / max_dist ** 2
    pixel[i, j] = lut[f]
                        

Radial

The radial gradient is a smooth transition of color along a direction of increasing distance to the center. To create the radial gradient you must define at least two color stops. You can also set a centre point and a maximal distance.

max_dist = normalize(start_point - end_point)
for each[i, j]:
    cur_dist = normalize(start_point - [i, j])
    f = cur_dist / max_dist
    pixel[i, j] = lut[f]
                        

Angular

The angular gradient is a smooth transition of color with growing the angle relative to start angle. To create the angular gradient you must define at least two color stops. You can also set a centre point and a start angle.

initial_angle = arctan2(start_point.y - end_point.y,
                        start_point.x - end_point.x) + m.pi
for each pixel[i, j]:
    cur_angle = arctan2(start_point.y - j,
                        start_point.x - i) + m.pi
    pixel[i, j] = lut[f]
                        

Diamond

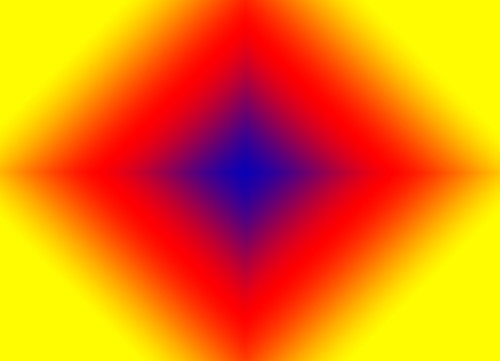
The diamond gradient is a smooth transition of color along a direction of increasing distance to the centre. But here L1-norm is used instead of L2-norm. To create the diamond gradient you must define at least two color stops. You can also set a centre point and a maximal distance.

max_dist = normalize(start_point - end_point)
for each[i, j]:
    cur_dist = sum(abs(start_point - [i, j]))
    f = cur_dist / max_dist
    pixel[i, j] = lut[f]